【塾授業から学ぶ受験対策】算数・図形を制するための先取り学習の重要性

中学受験を目指す家庭にとって、算数は合否を大きく分ける最重要科目です。その中でも特に多くの受験生を悩ませるのが「図形問題」。
今回は、実際に塾で行われた 図形の先取り授業 をもとに、受験に直結する学び方のポイントや、家庭での活かし方を整理します。

図形が中学受験で難関とされる理由

算数のなかでも図形分野は、次の理由から「差がつく単元」とされています。

実際、先輩受験生たちも「最後まで図形が一番苦手だった」と口を揃えます。
だからこそ、 早めの先取り学習 が大きな武器になるのです。

例えば、あるテストで娘は最初の計算を一つ間違えただけで、連続する3問すべてを落としました。
「最初の答えが次の問題の条件になる」形式では、 1つの誤答がその後すべてに影響 してしまいます。

👉 この経験から学んだことは、

ということでした。

塾の先生によれば、図形分野では小学生のうちから「分配法則」を意識すると計算が格段に楽になるそうです。

例えば図形の面積計算では、

といった工夫で 計算ステップを減らし、ミスを防ぐ ことができます。
中学生で本格的に習う内容を、小学生の段階で「先取り」することで、受験本番で余裕を持てるのです。

ノートに正確に書き写す

授業では「図を必ず自分で書き写す」ことを徹底していました。

こちらは、娘が図形を書き写したノートになります。

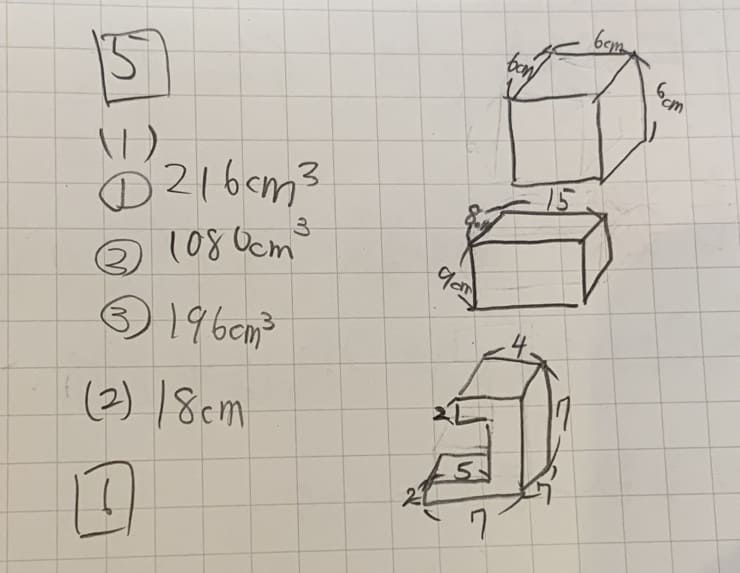
実際に娘のノートを見ても、板書をそのまま真似るだけでなく、線を引き直したり角度に印をつけたりすることで、 考えるためのヒントが自然と浮かんでくる ようになります。

この「手を動かして図を描く」習慣は、家庭学習でもぜひ取り入れたいポイントです。

授業では、多角形の内角の和の公式を学びました。

（角の数−2）×180°（角の数 − 2）×180°（角の数−2）×180°

例えば、

多角の角については、娘のノートにも、五角形と六角形に対角線が引いてあります。

このように、実際に多角形に対角線を引くことで「なぜこの式で求められるのか」を体感できます。
図形問題に強い子は、このように 公式の意味を理解しながら覚えている のです。

さらに授業では、5年生向けに「外角」や「くさび型」の角の求め方も扱いました。

どちらも 同位角・錯角の性質を応用 すれば導けるため、論理的に説明できるようにすることが重要です。

下画像は、娘のノートの「三角形の外角」と「くさび型」です。

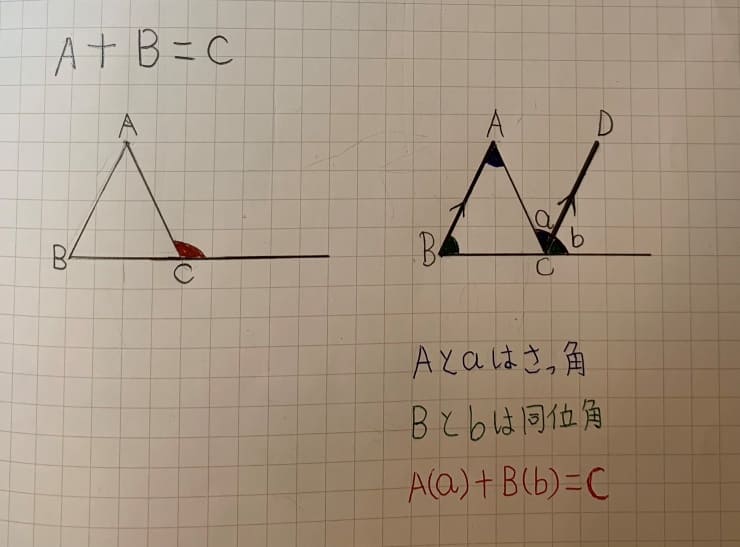
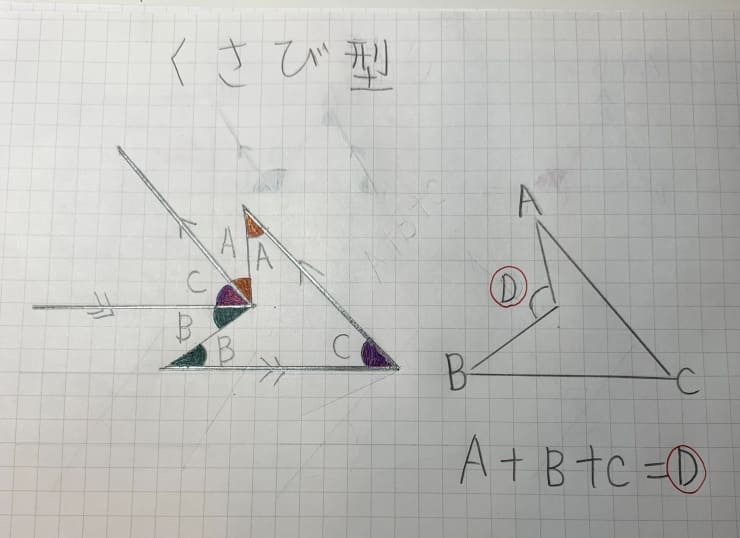
👉 ポイントは「答えだけ覚えるのではなく、導き方のプロセスを理解する」こと。

塾の先生からも「受験は夏休み中が勝負」と言われています。
特に図形は反復練習なしでは定着しにくいため、夏休みは じっくり図形に取り組む絶好の時期 です。

これらを徹底することで、秋以降の模試や本番に大きな自信を持てるようになります。

図形は「早めの先取り＋正確な理解」で得点源に

中学受験における算数・図形は、

という難しさがあります。

しかし、今回の授業で学んだように、

といった取り組みを積み重ねることで、図形はむしろ 差をつけられる得点源 になります。

夏休みは図形克服の大チャンス。親としても「計算ミスの連鎖を防ぐ工夫」や「学習習慣の支え」を意識して、家庭でのサポートを続けていきたいと思います。